Dear Parents – I’m Sorry For What I Said When I Taught Middle School

I loved teaching 7th Grade so much! 12 to 13-year-olds understand my humor better than most (not sure what that says about me) and I thought it was such a great time to get kids excited about learning math again.

That being said they also aren’t always easy to love – especially at home. So I sat in more than one parent meeting offering advice, telling parents about “homework time”, supporting their pre-teen, and all kinds of other nonsense that I thought was super helpful at the time.

As the mom of a middle schooler now I’d like to apologize for everything I said. Turns out I know nothing about raising preteens! After surviving the first month of middle school I’d like to apologize for a few things.

I’m sorry I thought you didn’t buy them paper.

I have already bought 5 packs of filler paper. None of it has made it into a notebook yet. It lives in his backpack until it becomes so crumpled it’s unusable. I’m sure he tells his teacher I don’t buy him any paper just like your kid told me.

I’m sorry I didn’t help them with their locker more.

Don’t get me wrong – I helped them learn to open their locker and unjammed it when it wouldn’t open but I didn’t really help them learn to use it. I didn’t explain enough about what to get and when, how to keep it organized, and how to check yourself to make sure you had what you need. Day 4 of school I had to make Jackson a checklist for the inside of his locker so he knew what in the world he was doing. I should have done that for your child.

I’m sorry I told you to have structured homework time.

I believe I even said, “even if they don’t have homework have them do something academic during that time”. Our evenings are a DISASTER. Jackson doesn’t get home from football practice until 7:00 (and later if they have a game). Our structured homework time usually goes like this “Jackson let’s rush through your homework while I shove dinner down your throat and you shower all at the same time”. All the while he is crying because he wants to be outside playing with his friends. I should have just told you to do whatever you can to survive (and not assigned any homework).

I’m sorry I didn’t keep you more updated on what was happening at school.

I know middle school is the time of independence and I treated it that way. I began to encourage kids to email me about missing assignments, questions about work, and other issues instead of their parents. I wanted my students to be the leaders in their learning (and I want that for my son too). But I do miss knowing more about what’s happening and being a more active part in school and what’s going on.

I’m sorry I didn’t tell you more how awesome your child is.

Middle school is hard. Middle school parenting is harder. You are doing a great job and I know that because I got to spend 7.5 hours a day with your child. As a parent, I feel like I am failing a lot. I see the attitude, the not wanting to do homework, and the power struggle. I don’t see him asking questions, engaging with his peers, and being a positive active kid at school. I should have told you more about all the good that was happening at school so you could hear just how awesome the human you are raising is.

I’m sure there are a lot more things that I haven’t even realized yet that will come to me as our middle school experience continues. For now, I will keep learning and struggling. Most days I am positive that teaching 120 middle schoolers was way easier than raising 1 of them. When I return to the classroom one day I will surely be a better teacher and more understanding now that I truly understand the parent’s perspective.

I’m really sorry for what I said before I knew.

Mathematics as a GateKeeper – My Story

This may surprise some people that are online friends and acquaintances but I am super socially awkward. That awkwardness paired with my anxiety means I spend countless hours worrying that I said, did, or thought the wrong thing and will forever be an outcast as a result.

Don’t worry this blog post isn’t about unraveling all of those issues but it is key to understanding the many ways in which the math classroom served as a gatekeeper for me in social situations and how in many ways math only contributed to my issues as a preteen rather than helped them.

You’ll also need a basic understanding of how I grew up. I was raised on a family dairy farm which for those of you not aware is a 24 hours a day/ 7 days a week job. We lived 25 minutes from the town where I went to school which was a long way when your parents had a lot of chores and work to do and although I am now so thankful for my upbringing and the opportunities I had as a result – as a 12 and 13-year-old girl I wanted to be like the other kids and not a farm kid.

The other girls in my class had families that vacationed together (we couldn’t take family vacations because someone had to be at the farm to milk), frequently hung out together after school and on the weekends (I didn’t want to ask my parents to drive me back and forth to town), and were involved in lots of activities (again the distance and time issue).

My one chance to try and hang out and be normal with the other kids was at school each day but once the all-important middle school grades hit there was another hurdle standing in my way – math class. 7th Grade was when our school began sorting us very clearly into the haves and the have nots of math and lucky me straddling the gate between the two. I remember being determined to make it into Advanced Pre-Algebra as a 7th grader. If I didn’t it would be just one more way that I was different than the “cool kids”.

By some luck, they let me in but it meant that I had to go to a 2 week Pre-Algebra camp that summer – yes that’s a thing. I remember feeling really bad having to ask my parents to drive me back and forth to school every day for those 2 weeks (there was no bus) but I really wanted to do whatever it took to be normal and get in the class. It was clear early on that I was struggling but I was determined to make it.

I made it through Pre-Algebra that year with a C and against the teacher’s recommendation went on to Algebra I in 8th grade where the wheels fell off and I wasn’t allowed to move on to Geometry in high school. I would have to retake Algebra I. Dream over. My only chance at being in the “cool kid group” over because of math class.

I was pretty much done with math after that. I did well enough because my parents expected good grades. I remember being bored a lot because I knew how to do the math but simply looked at it in a different and that wasn’t ok in the 1990s. I also know I completely shut down in regards to trying to understand what was happening which really came back to hurt me once I started Pre-Calculus and had no idea what was going on.

If you could have polled my teachers I would have been voted “least likely to be a math teacher” instead I was voted “most likely to be a talk show host” (there’s something that makes you feel intelligent!).

I went to college became an agriculture teacher and lived happily ever after until I realized that I was explaining math to kids in my ag class that were struggling in the traditional math classroom and that I wanted to help them have a fate different than mine. I didn’t want them to give up on it like I did.

So I went back to school to teach math – this time feeling like a success rather than a failure. What a difference that shift in mindset made.  For the first time I really began to understand what was happening and the why behind the math I was doing. I remember the first year I taught Algebra I when I would spend my evenings studying so I was on top of my game for the next day. I myself area models that year for the distributive property to teach polynomials and my world was rocked. For the first time FOIL went back to being something that belonged in the kitchen rather than something I memorized to pass a test.

I have realized in the years since then what a gatekeeper my math experiences really were for me. I have no regrets about where life has taken me but what would have been different if my mathematics education had been more positive? What if I had been encouraged in math rather than being held back? What if I had felt successful rather than always feeling behind? Would I have thought about a career in engineering, as an analyst or in data science? Would I have approached college mathematics classes differently – pursuing them rather than doing my best to avoid them?

How many kids are sitting in classrooms just like me? Desperate to be in the “good math class” so they can be with the peers they so desperately want to be with and then devastated when the fall short? There has to be a better way to keep kids from feeling as though math the gatekeeper that is stopping them from reaching their goals.

 

Something Bigger – Keeping Our Book Project Going

It started as a simple idea…Kevin and I were older and more established when we got engaged. We didn’t need sheets or pots and pans so we thought “let’s find some teachers and let them register for school supplies”. We thought we’d give away some markers and glue, feel good for a few weeks and move on.

Then my friend Erin asked if she could register for books for her high school Freshman to take home and own. Most had never owned a book of their own or read books where they could see themselves in the characters. She selected racially diverse books with characters and storylines kids could relate to and let each student ask for 3 books from list.

Generous friends, family, and strangers from around the country filled our garage with books…over 400 of them. Enough that each of Erin’s students got to take home 3 books before summer break that they would never have to give back, that they could keep forever, and that would hopefully set them on a path to start reading more.

The day we gave out the books I had to try hard not to cry. The kids, 15 year olds, struggled to understand that they didn’t have to give the books back. They made plans with Erin about how to keep their books safe until they got home so that they weren’t taken by other students. They brainstormed about how they could “trade” books if they finished reading one of them before summer break. It both filled and broke my heart at the same time.

In the days since we have heard feedback from the kids like, “I’ve never read a whole book and I read that one in a day”, “I didn’t use my phone the whole weekend”, and “I already read 4 books”. It struck me how many of these kids had probably never been able to identify with any of the books read in their classrooms. I also thought back to many of the students I taught who hadn’t been able to check books out of the library for years due to fines and lost books. When your family is choosing monthly whether to pay the light bill or the electric bill paying $16.00 for a lost library book isn’t a priority.

I left the high school that day knowing this project couldn’t end with this group of kids or this high school. So here I am asking for your help again. Kevin and I are going to continue collecting as many books as we can in order to keep these book gifts coming. Although I am not sure how many books we will collect or how many students we will help I know that kids are worth us taking the risk.

We will continue collecting and organizing the books in our garage and paying the expense of getting the books wherever they need to be. We’ve created a book list for middle and high school here with the help of Project Lit and my friend Erin. For now we have decided to focus on middle and high school students as there are quite a few book programs currently for elementary students and Kevin and I are just two people. Maybe one day we will be able to expand – a girl can dream.

If you want to order a book off the list it’ll be shipped right to us. If you have copies of these books that you’ve read and loved that you want to donate send me an email at lindsaybrookepowers@gmail.com and we will help you get it to us. I encourage you to write notes to the kids in the books if you want to, everyone needs a kind word from time to time and maybe your words will help change a life. If you have suggestions of a school that would benefit from books send that to me as well. I don’t know how long it will take for me to get enough to deliver to a school again but I have faith that we will get there.

Maybe we are crazy but I also know the best ideas come from just a touch of crazy. I also know that kids are worth it. I hope you’ll help me spread the word and let’s turn this into Something Bigger.

Filling Your Own Bucket

So many people I talk to have been dealing with burnout lately. Unfortunately I haven’t been immune to that either and am the first to admit I haven’t been on the top of my game lately in many ways.

This week’s #OpenUpMath chat dealt with self-care and really caused me to pause and reflect on what was causing this funk that I have been in.

I have been lucky enough to go to a lot of conferences lately and meet a lot of awesome people and that is something I definitely don’t take for granted. The only problem is I was there working not learning and didn’t spend anytime actually attending sessions.

One thing I have figured out about myself as of late is that I am definitely someone who has a need to keep learning. It is what feeds me. I want to be one of those people who gets their inspiration by running (if you ever saw me run you’d laugh) or meditating (hello talking to myself for 10 minutes waiting for “meditation time to be over”) but it just isn’t me. I draw my inspiration from learning new things.

But I am also realizing that in the past I have learned and drawn inspiration from things that make me “feel good” and not necessarily  things that help me grow or push my thinking. When I am at a conference I go to too many sessions because I know the speaker, because everyone else I know is going, or because it is something familiar to me and not nearly enough because I know it will challenge my status quo.

Thank goodness for Twitter and the edu people there who have really started pushing me beyond my comfort zone and into becoming a stronger leader who recognized my many shortcomings and faults. Two weeks ago #OpenUpMath chat was about books for professional learning and this week it was about self-care and the timing of those was just what I needed.

I am committing myself to dedicating time each day to read books that push me beyond my normal thinking. Just saying I am going to do it isn’t enough. I said two weeks ago I was going to start and didn’t so I am going past that and literally putting time on my calendar each day to study and sharpen my own brain so that I can be better for the people and communities I serve. (In other words it’ll be less meetings more readings!)

What are you committing to do to fill your own bucket? I’d love to hear!

More Than a Mission: AKA How You Know We Have a Problem in the Edu World

At least once a day (but usually many more) someone comments on my ridiculous drive to work hard, do all, and see all in regards in education. I’m the first to admit that more often than not I find myself pushing past the point of exhaustion to get one more task done, read one more edu blog, or watch one more hour of our Kentucky legislature. This week alone I came home exhausted on Tuesday from an amazing experience with Open Up Resources at ASCD to a full inbox, a backlog of tasks, a National PLC meeting one evening, and National Book Study the next. This weekend I have another PLC meeting on Saturday and a Book Study on Sunday – no rest for the weary right?

So why push myself so hard? Why sacrifice fun and family time for people I have yet to meet in person and may never get the chance to?

Because teachers and kids are worth it and they need someone to help be their voice.

When a Principal Gets in Trouble for Following Reading Research We Have a Problem

While I was at ASCD I had the chance to talk with a wonderful principal who was at a school in a district that adopted a “big box” (and also unaligned and low-quality according to EdReports) curriculum. His school serves a highly diverse population and many students that come from a low socio-economic background. Much like all of the great research Eduvaites has been putting together this principal saw the the curriculum was severely lacking in phonics instruction so they began supplementing.

You won’t believe what happens next…

The district came in and told them to stop supplementing. They were told that if it didn’t come in “the big box” they weren’t doing it. Insert shocked and angry face here!

I have to keep working hard spreading the word about aligned and high quality curricula so that principals like that can serve their students in the way they want without getting “in trouble” from their bosses.

When a Teacher is an Island We Have a Problem

Then there are the teachers that have no curriculum at all. I have met some of the most amazing teachers from around the country this year. So many of them are at very small districts where they are truly an island. There is no mandated curriculum, they can truly do whatever they want and they want to do amazing things. Do you know how hard it can be to do amazing things when there is no one to talk to or plan with?

These teachers have found a “home” in the Open Up Resources 6–8 Math PLC Community. They have been able to chat daily via social media and meet monthly via video chat with other teachers from around the country to plan, reflect, and think deeply. They aren’t alone anymore and that is priceless to me.

When Teachers Are the Vilians We Have a Problem

And I can’t forget my Kentucky teachers. They have been bullied, threatened, and thrown under the political bus for the last year here. Sadly I can’t do nearly as much to help them as I would like but I have been able to watch every minute of Education Committee meetings that have been broadcast and as much of the General Session as I can to stay informed and updated about what is going on in our state capital. Watching the corruption, lies, and backdoor dealings have affected my psyche greatly. My husband tells me frequently to just turn it off but I can’t. I have to stand up and watch for those who are teaching our kids and can’t watch for themselves.

When in 2019 We are Still Marginalizing Others We Have a Problem

As a part of watching all of our political coverage and learning from some brilliant voices like Marian Dingle I have also been doing a lot of reflecting on the marginalized people and voices in the education world. I have no doubt that there is a lot I have done wrong in my life that have contributed to this marginalization. I also know I am more privileged than I deserve and continue to do a lot of work on the language and work I do to ensure I don’t further the marginalization of others by making assumptions and or refusing to give up power.

On one of the last day’s of our legislative session I was moved to tears watching this exchange between Representative Charles Booker and Speaker of the House David Osbourne. I was a fan of Booker before as he has been a huge advocate of public education but this exchange taught me a lot more about marginalization and privilege. I challenge you all to watch it as Booker is called out of order and his microphone is eventually turned off for doing no more than speaking his truth.

I have to continue to work hard to recognize my own white privilege and do whatever I can to bring more awareness of marginalization to the edu space and Kentucky as a whole. We can and must do better.

We Can’t Stop Won’t Stop

Why do I work so hard? Why do I go days without enough sleep or taking care of myself? Because all of these people and so many more deserve better. I may just be one person but I also have the best virtual community on the planet. Together we can’t stop, won’t stop.

 

 

It’s Not as Simple as Holding Back 3rd Graders

Thanks to the continued shadiness of the Kentucky General Assembly I have been watching hours of committee meetings and chamber sessions to stay on top of what our Legislature is up to this session. Needless to stay my mind stays blown and my blood pressure stays raised most days.

One of the bills that has really piqued my interest is regarding mandated testing of 3rd graders for math and reading fluency and then holding back every child that doesn’t meet the standard in one of the areas.  I get it – at first glance maybe this sounds great and like it makes perfect sense. Of course I want all kids reading and doing math on grade level. I’m not crazy.

The problem isn’t wanting kids to be proficient in reading and math by the end of 3rd grade, the problem is that the bill doesn’t address how to fix the plethora of issues that cause kids not to be on grade level in the first place.

First, there is no proficiency test written yet and no one seems to know who would write it, when it would be ready, or where the funding would come from for printing, administering, or scoring this mandated test. In the session the other day it was brought up that the group they asked to write the test said they had no one qualified to write the assessment. Cart meet horse.

Then we have the fact that no funding is included to better help teachers in making sure students are meeting grade level standards. Teaching is a science and teachers need up to date trainings and professional learnings yet our General Assembly has continued to slash funding for these opportunities. Most districts barely have professional learning funds at all much less the amount required to invest in this kind of training.

One also can’t forget about the curriculum disparity issue. There are districts across the state of Kentucky using unaligned and low quality curricula that do not meet grade level standards  or address the need for phonics instruction. The bill of course provides no provisions, mandates, or funding for this either. Luckily thanks to the OER movement there are more and more high quality curricula on the market at low or no cost available to districts but there are many districts still not using these options. I have recommended more than once that districts and Superintendents be held accountable for adopting and using low-quality curriculum but the legislature doesn’t seem to want to adopt a mandate like that…a quick look at companies that spend 8+million dollars lobbying legislators each year will give you a big idea why.

And then there are the other questions.

I also keep thinking about what happens when 50% of a school’s 3rd grade doesn’t meet 1 or 2 of the benchmarks. Do we hold back 50% of a grade level so that next year instead of 120 3rd graders we have 180? What if the next year there are then 270?

What if a student doesn’t meet the benchmark the 2nd year? The 3rd?

What about our ELL students?

What about students brand new to our country in 3rd grade?

What about the refugees I taught that experience significant trauma?

What about our students with disabilities?

See I don’t have the answers to all of these things but neither does our legislature. Passing a bill doesn’t miraculously answer these questions. Instead it puts another testing requirement on students who already have end of year state assessment and more pressure on already over worked teachers. I do think there are mandates and requirements that could benefit students and districts but those aren’t the ones legislators are willing to pass because that would affect those putting money in their pocket.

Here’s what I do know though – It’s not as simple as just holding back 3rd Graders.

Data Teachers Really Want – Hint: It Doesn’t Come In a Dashboard

I have been thinking a lot about data lately. Especially the difference in the data teachers want and actually use vs. the data districts seems to make their curriculum decisions around. I saw first hand how a district could be “wowed” by fancy data dashboards with a multitude of reports, settings, and options but I also never saw my district make great use of these reports. The question keeps coming to my mind – why do we adopt less than stellar curriculum at an excessive cost just for the bells and whistles that come on these data dashboards?

I know the data that I used frequently as a teacher to inform instruction and none of it came from a dashboard (with the exception of the Desmos Teacher Dashboard which is free and formative so totally different ball game!) However, since I am not currently in the classroom I don’t want to speak for teachers without asking what they are doing first so I took to Twitter to ask them.

They had some awesome ideas about what they used in their classrooms to monitor student learning and achievement but none of them came in the form of a flashy data dashboard like I’ve seen some school district make curriculum decisions based on.

This slideshow requires JavaScript.

So my sincere question is this – should school districts be making decisions influenced by the inclusion of data dashboards if it isn’t the data teachers really need and use?

As a parent it also concerns me that my daughter, who is a struggling reader,  uses a reading program that only partially meets expectations on Edreports but comes with fancy assessments and dashboards so was chosen my our district. I would gladly trade her having the opportunity to learn from a highly rated, aligned, and coherent curriculum that is based on science than her district have even more data to show that she is behind in reading. Perhaps with a stronger curriculum she wouldn’t be behind in the first place.

I’d love to hear others thoughts on this topic! I am still working through the disconnect between what teachers actually use and what school districts want in regards to data in my own mind as both a parent and a teacher so opinions welcome!

 

Good Curriculum Matters: Here’s Your Proof

In October of last year I started having nightmares about our state assessment scores coming out. I had pushed (and hard) for my school to pilot Open Up Resources 6–8 Math and it was a huge transition for our teachers. I think October was when it hit me that if it was a flop that I had put my school, colleagues, and students in a terrible position.

I knew in my soul that it was the best way to teach math but you know there is this “little” thing called accountability testing that meant regardless of what I thought that if the kids didn’t perform well on state testing that I had bought myself a lot of trouble. October was about the time of year that we were worried about pacing, the transition to a program that was so conceptual, and the million other things that comes with adopting a new curriculum hence the nightmares I started having.

There were bright parts along the way that I blogged about. We really saw the beautiful part of teaching students conceptually and had some amazing student outcomes on our MAP testing but I knew none of that mattered if my kids didn’t perform on our state test.

I got word in September that our results were strong but since I was no longer employed in the Fayette County School District it was so hard to get detailed results. Finally this morning our state department of education went live publicly with 2017-2018 detailed accountability data so I immediately dove in to see just how impactful the curriculum was.

I did a lot of analysis this morning and I am so excited to share it with you. A few quick notes. This is our 7th grade data only. Our 6th grade math also had strong results but since I was a 7th grade teacher I felt I could speak most accurately to the teaching and learning in 7th grade so I chose to focus on those results. There were also some long term teacher absences in 6th grade that I felt may have skewed the data somewhat and I wanted to present the best data I could for those interested.

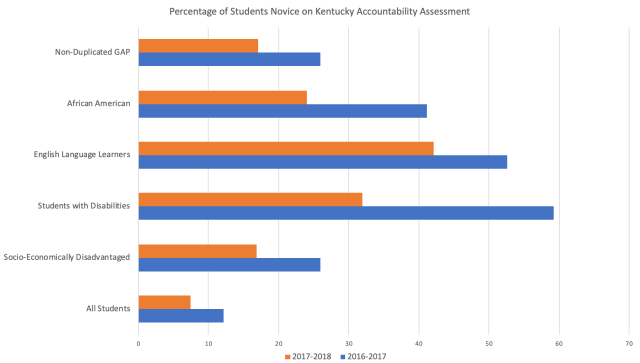
This data is a comparison of 2016-2017 and 2017-2018. In that time our 7th grade teaching team remained the same so there was no difference in teachers. The demographic in our school also did not change significantly in that time. Although our state accountability system is undergoing some changes the test and measures of Novice and Proficiency did not. All of this data is based on 326 7th grade students who were tested. If you have other questions drop them in the comments I am glad to answer them.

Here we go…

 

All Learners –  the percentage who were Proficient/Distinguished increased by 15% while the percentage who were Novice decreased by 39%.

Economically Disadvantaged Students – Proficient/Distinguished increased by 34%, Novice decreased by 35%

Students with Disabilities – Proficient/Distinguished increased by 8%, Novice decreased by 46% (did you read that…wow!)

English Language Learners – Proficient/Distinguished increased by 100%, Novice decreased by 20% (this is probably what I am most proud of…we doubled the amount of English Language Learners that were Proficient of Distinguished on the state assessment!)

African American Students – Proficient/Distinguished increased by 50%, Novice decreased by 42%

Non-Duplicated GAP – Proficient/Distinguished increased by 26%, Novice decreased by 32%.

 

So there you go, year one of  Open Up Resources 6–8 Math. I am still in a little bit of awe at how much the GAP actually closed. I can’t help but think if we made this process in year one what schools in year two and onward will be able to do for students.

Kids, all kids, deserve a chance to be successful in math. Two years ago if you were a student with disability in our school there was a 60% chance you were Novice on the state test. Last year there was only a 30% chance and that was with only 1 year of strong curriculum. It gives me chills to think about what can happen to a student over the course of 3 years with a strong math curriculum like this one.

Good curriculum matters. Here’s your proof.

Sources:

2017-2018 School Report Card

2016-2017 School Report Card

 

Answers to Your Questions 1/24/19

There were some great questions asked about this data that I wanted to address! A teacher on Facebook asked a great question wanting me to compare last year’s 7th graders with their 16-17 6th grade scores rather than the previous class of 7th graders. I did that and WOW.

Check that out… a 322% increase in our ELL students Proficiency from 6th Grade to 7th!

Dan Meyer also asked some great questions that I wanted to address:

Hi Brooke – these are really fantastic results, particularly if y’all think the K-PREP is a good exam. Thanks for sharing. Can you elaborate a bit on the factors you think led to those results? I’m sure good curriculum is a part of that. Were there other parts? What was the teacher PD like? What kinds of communities of practice would we find in FCPS? Did you folks do a lot of hiring in seventh grade math last year and if so what kinds of teachers were you looking for? Basically whatever you’d be willing to share in whatever time you have would be a big service to the math ed community.

 

My response:

Those are GREAT questions that I am happy to answer and will also go back in and add some of that information as an addendum so others can find it easily.

I do not honestly find that K-PREP is a good exam but it is what we have and it did provide a good comparison for me to use. Previous to 2017-18 our results were pretty consistent. We did not experience any large jumps or drops in scores like we saw here. I have written other posts on different assessments including NWEA’s MAP assessment where we also saw huge growth for all learners – especially those in the GAP and also our district written assessments so thee results really have been confirmed in a variety of ways.

I wish so much that we had strong PD around the curriculum. I can’t imagine how much growth we could have seen had we been able to take advantage of that. But we were really on our own in the District. We were the only school using Open Up Resources 6–8 Math and they helped us purchased the books but then we were on our own. I provided a PD to the teachers before school started to introduce them to the materials and any routines they were not used to but that was all we did in that regard. We had monthly Department meetings and weekly PLC meetings however where teachers could brainstorm and problem solve.

I will say one advantage we had was that I had long been an active MTBoS follower so I was very familiar will the instructional routines and structures such as Which One Doesn’t Belong and Notice and Wonder. Over time, I had introduced many of those to our Department in meetings and summer PD so they weren’t starting from scratch which I imagine would have made it much more challenging.

FCPS does have a wide variety of teacher PD days where teachers are “released” from the classroom for a day for professional learning. They range on a variety of topics and our teachers did participate in those but their participation was no different than it had been in years before. Things in FCPS remained the same as they had been in prior years.

We also did not hire any new seventh grade math teachers. The seventh grade team had worked together for the last 4 or 5 years with no changes at all. We did bring on a new collaborating math teacher in our co-taught classes. She was not new to our school building but was new to our PLC.

Our student population did not experience any large changes in this time either.

Another teacher asked what I thought was a very valid question. She wanted me to compare same students to same students. So instead of 16-17 7th graders to 17-18 7th graders she wanted to see the 17-18th graders comparison to their 6th grade scores from the previous year. I crunched those numbers and the results were crazy. I will add in that chart but our ELL students experienced a 322% growth as they moved from 6th to 7th grade. Of course maybe this can be attributed partly to them having an extra year of language experience but I was so excited for them regardless. They are closing their GAP and that is what matters to me.

Overall, I think the biggest impact was the fact that we went from no curriculum to a top notch curriculum in one year’s time. Although we had the best of intentions and worked ourselves hard to plan engaging and coherent lessons the truth is we obviously fell short especially when it came to coherence. I had long been a supporter of teaching math coherently and thought I was doing it…until I started using Open Up Math and then I quickly discovered that that kind of planning and forethought was something I just couldn’t easily achieve while also teaching full time and all of the responsibilities that come with that. In short it is pretty near impossible to be a full-time teacher and a full-time curriculum writer which is what I had been trying to do for 12 years. For the first time I could really focus on my teaching and the kids learning. That’s a simple though but had a monumental impact. I could refine my craft as a teacher instead of resource mining and piecing together part of other curricula to put something together that I thought served my kids.

From my students standpoint I think the greatest contributor to their success was math through this curriculum became something they enjoyed more because they had more autonomy in their problem solving methods and strategies. I was never a “hey you have to do this my way” teacher but I will admit a shameful teacher truth – when push came to shove and we had been on a topic way too long and my GAP students were still struggling I would try and make things easier for them by breaking things down, showing them steps, and giving them ridiculous things to remember. I am not proud but I was desperate sometimes.

The cyclical nature of Open Up Resources 6–8 Math meant that when we had spent a lot of time on a subject and we weren’t quite to mastery that I knew that the topic was going to continue to be woven in the next lesson and unit so that my students could continue to grapple with the math until they achieved mastery in their own time. I had so many struggling students for the first time tell me that the really “enjoyed math class” and I attribute that to the fact that it was no longer a race to mastery but was instead a time to brain storm, problem solve, work together, and think.

I saw that often when it was time to take a high stakes assessment. The kids who would previously “do math” by taking all the numbers out of a problem and add, subtract, multiply, and divide until they got something close to one of the answer choices and then decided that must be it were instead making xy tables, drawing number lines, using tape diagrams, and really reasoning. That was a win for me as a teacher. Half the battle of teaching math is convincing the kids that they can do it, this curriculum really did help me do that.

Sorry this was a novel. Hope this helps. Shout with other questions!

If 2nd Graders Bowled Like Legislators Passed Laws

I had the chance to go on my 2nd grade daughter, Embry’s field trip to the bowling alley today. I won’t lie, I had my concerns. Bowling isn’t easy – especially when the balls weigh 25% of your total body weight like Embry but I had the best time watching the kids interact.

I thought there would be upset kids and hurt feelings over gutter balls, low scores and the kids that were way better bowlers than others. Instead I heard a lot of this:

• You knocked down two pins that is so good!
• Here I’ll push the ball with you.
• Let me hand you the ball when it come out.
• Ms. Powers did you see ______ knock all the pins down? That was so cool!

In fact in the time we were there I didn’t see any hurt feelings or being upset over how bowling was going. They were more concerned about their group as a whole than their individual performance.

Seeing this came at a really good time for me after watching the performance of our government in our special session over the last two days. I started thinking on my way home, what if these 2nd graders bowled like our legislators?

Governor 2nd Grader: I know we are going on a bowling field trip we’ve already paid for in 3 weeks but I am paying lots of extra money so we can go today.

Teacher 2nd Grader: Well we think that’s ridiculous but we will be there to make sure that you don’t cheat.

Governor 2nd Grader: No need to be there I will bowl for you all. You aren’t good enough to bowl. You’ll get more pins this way.

Teacher 2nd Grader: We’ve just seen you all cheat a lot and we’d like to make sure that doesn’t happen again.

House Leader 2nd Grader: Before I roll this ball I am going to give a 10 minute speech about what is wrong with all of you teacher 2nd graders. We’ve cheated at bowling for 55 years and no one has cared. Now that we’ve been caught you all are all worked up about it. I’m here to tell you that we cheated today the same way we cheated last time and the same way we will cheat again next time.

Majority Party 2nd Graders: Yes most of us were here when all the cheating you teachers started to begin with and yes we went along with it but that’s before anyone knew what was going on. Stop asking us hard questions or we will quit. Isn’t there a private room we can bowl in? When is recess?

Minority Party 2nd Graders: They won’t even let us play the game anymore.

Majority Party 2nd Graders: I am not sure we will win the game so we are going to quit. We will come up with a game that those teacher 2nd graders definitely can’t win before we come back here again.

Welcome to the picture of maturity in Kentucky folks! All that was in good fun but not true far from the truth about what is going on here. I highly recommend wherever you are located that you start watching the coverage from your state legislature. You will be shocked at the shenanigans that go on each and every day.

Stay informed and stay active. I vowed to be a voice at the state level for the kids who don’t have one and I don’t take that promise lightly.

My Mama Says Nothing Good Happens After 10pm…Why Didn’t Anyone Teach the KY House Leaders That?

I had a lot of time to think last night – mainly because I was afraid to go to sleep. In Kentucky our legislators seem determined to only do business behind closed doors and in the dark of night so I am forced to stay awake odd hours, check the Legislative Research Council Website, and social media to stay informed about what is happening in Frankfort.

My mom always told us as kids that nothing good happens after 10pm. I wish my legislators followed that advice.

I was also worried for my kids all night. It was unclear most of the night whether there would be teachers to teach them today. Embry was excited to make gingerbread houses with her beloved 2nd Grade Teacher and Jackson is wrapping up his Colonial Times unit by participating in “Barter Day” where he carefully selected 5 items from home to try and trade with his classmates for other goods like in Colonial Times. It would have broken their hearts to miss school today, as it will if school is cancelled tomorrow and the have to skip their end of the semester bowling trip or “Colonial Day” filled with colonial crafts and activities.

However, as a former teacher I will gladly take on explaining to them why there is no school tomorrow if it comes to that. There was a a different air in the car circle this morning when the kids got out of the car that truly gutted me a bit. I saw, for the first time, a look of defeat on the teacher’s faces. They are tired too. My guess is they also were afraid to go to sleep last night. My guess is they were worried sick about how upset their students would be if they had to miss all the end of semester fun. I bet they worried about who would explain why there was no school to the kids who don’t have a loving home environment.

I think in many ways teachers are too tired to even be upset about what is in the crazy pension bill at this point. But I do think they are upset and worried for their students.
I think they are worried about how you teach kids to be good losers when our Governor just showed that when you lose instead of accepting it you throw a fit until you get your way.

I think they are worried about teaching kids to follow the rules when our legislators last night voted to “suspend the rules” so they wouldn’t have to follow any in regards to passing this bill in special session.

I think they are worried about teaching kids about democracy and using your voice when I myself have emailed my legislators respectful and solution focused letters nearly daily since the first of November and have yet to get a response.

I think they are worried about teaching kids about the legislative process when only one party has been allowed to see a bill that will effect so many people.

I think they are worried that the public will buy into the rhetoric and drama and not see what is going on behind closed doors.

I think they are worried that all the good they do each and every day will be forgotten and their legacy will be this one moment in time.

I see you worried teacher and this parent supports you.

Nothing good happens after 10pm. Or behind closed doors. Or in secret. Or in expensive special sessions. Remember that Kentucky.